Those of you who have read previous articles of mine already know that I like tricky questions – especially if they don’t look too complicated in the first place. Here’s one for you to try: Does the penny make a half or a full rotation when rolling it around another penny?
Would you expect Mr Lincoln to show his head upside down?
It was really surprising for me when I thought about this kind of operation, namely division by arithmetic means and expected values. People tend to work with means and expected values very intuitively. You can add and multiply them without any issues. Dividing on the other hand can be misleading and I am going to illustrate this with some neat examples.
Imagine that a friend of yours would like to play a game. Your friend writes down two different numbers on two separate slips which you cannot spot. Afterwards you are allowed to choose one of the slips and read the number written on it. The game’s goal is to make a rough guess on the value of the second number.
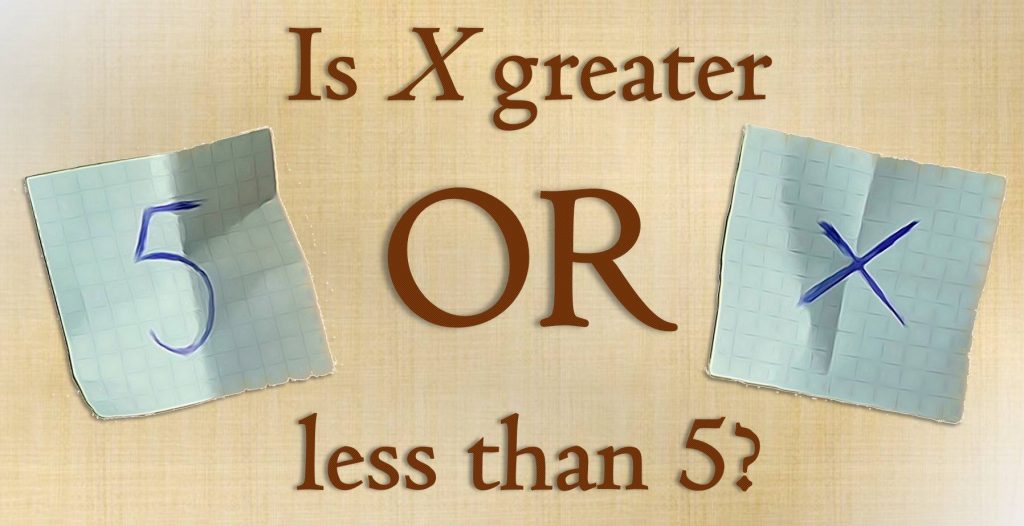
You think there is a 50:50 chance for guessing correctly? Although you may not believe it: The probability for a success is definitely higher when you apply the following strategy! more →
I guess that you already know a little bit about hypothesis testing. For instance, you might have carried out tests in which you tried to reject the hypothesis that your sample comes from a population with a hypthesized mean µ. As you know that the sample mean follows a t-distribution (or the normal distribution in case of huge samples), you can define a rejection region based on a specific significance level α. In a one-sided test, sample means which are less than a critical value CV might be considered to be rather unlikely. If the obtained sample’s mean falls into this region, the hypothesis gets rejected at this particular signficance level α.
Distribution of sample mean and rejection region for one-sided test
We know the chance of rejecting the hypothesis although it’s true (Type I error), because it is the chance of obtaining just one of those values from the rejection region (plotted red). But how likely are we to reject a hypothesis if it’s indeed false? In other words: How small is the type II error? more →
Integration by substitution (often referred to as u-substitution) is quite hard to understand. Most people just follow their proven recipe when performing this kind of integration. In contrast to that doing, I want to illustrate why the steps of u-integration are necessary. Therefore we will develop the idea slowly by giving simple examples which illustrate what works and what doesn’t. more →
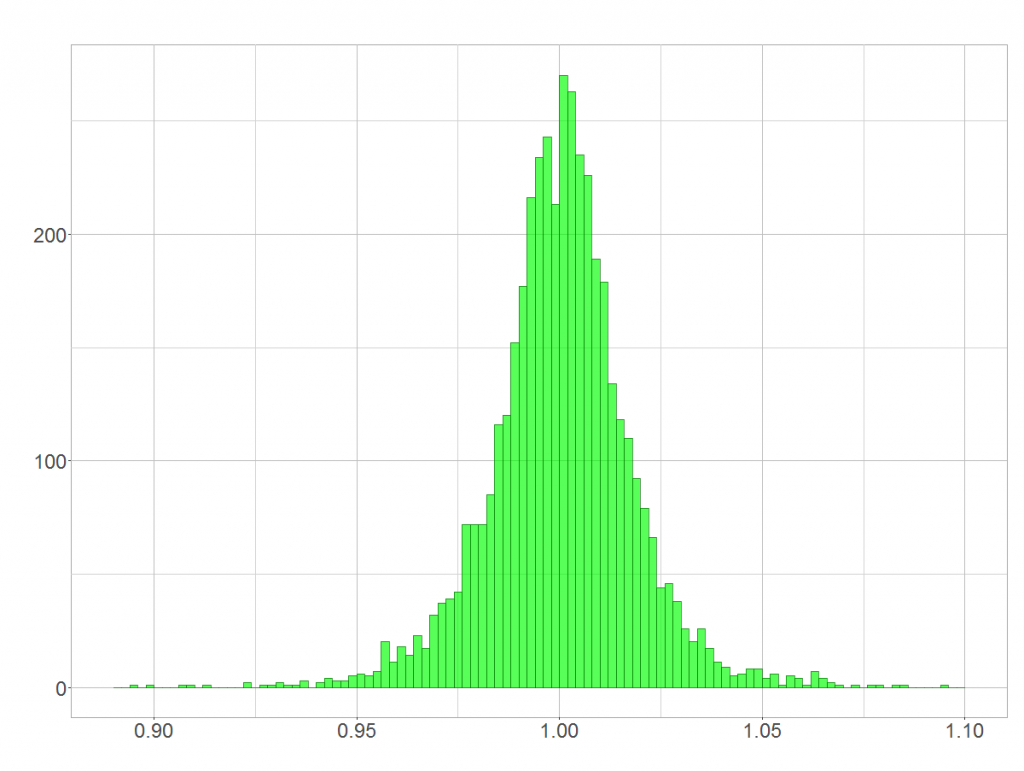
Quick question: Is BASF’s day-to-day rate of stock returns (shown below) distributed normally?
Day-to-day rates of return of BASF stock
Yes? In theory it isn’t! In theory rates of stock returns follow a lognormal distribution as I have shown in “On the distribution of stock return”. Unfortunately, most people don’t take the lognormal distribution serious, although it is very often at work! This article shows how the lognormal distribution arises and why its shape sometimes mistaken for a normal distribution. more →
There are many applications for the arc length of functions. I came across it when I needed to calculate the length of a density function in an interval ![[a,b]](http://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0 "[a,b]")
Do you grasp how this formula arises? No? Let me show you! more →
One of statistic’s foundations lies in the fact you can add variances. Maybe you wonder a little bit, because the formula for the variance does not look like that at first glance. This article will show you the proof why and under which circumstances adding variances is a valid practice. Please check the information given in my articles on addition and multiplication of expected values, if you do not have collected experiences with it yet. more →
© 2024 Insight Things
Theme by Anders Noren — Up ↑
![\displaystyle s=\int\limits_{a}^{b}\sqrt{1+\big[f'(x)\big]^{2}}\,dx](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+s%3D%5Cint%5Climits_%7Ba%7D%5E%7Bb%7D%5Csqrt%7B1%2B%5Cbig%5Bf%27%28x%29%5Cbig%5D%5E%7B2%7D%7D%5C%2Cdx+&bg=ffffff&fg=000000&s=0 "\displaystyle s=\int\limits_{a}^{b}\sqrt{1+\big[f'(x)\big]^{2}}\,dx")
