Imagine that a friend of yours would like to play a game. Your friend writes down two different numbers on two separate slips which you cannot spot. Afterwards you are allowed to choose one of the slips and read the number written on it. The game’s goal is to make a rough guess on the value of the second number.
You think there is a 50:50 chance for guessing correctly? Although you may not believe it: The probability for a success is definitely higher when you apply the following strategy!
A surprising strategy
The first step of the strategy is making up a random number M. If M is greater than the known first number, then guess that the second number is also greater than the first number. If M is less than the first number, then guess that the second number is less than the first number too. “And how does this help with the probability?”, you may ask. Imagine we knew the second number. With the first number F and the second number S we obtain 6 constellations arranged in 3 cases as illustrated below.
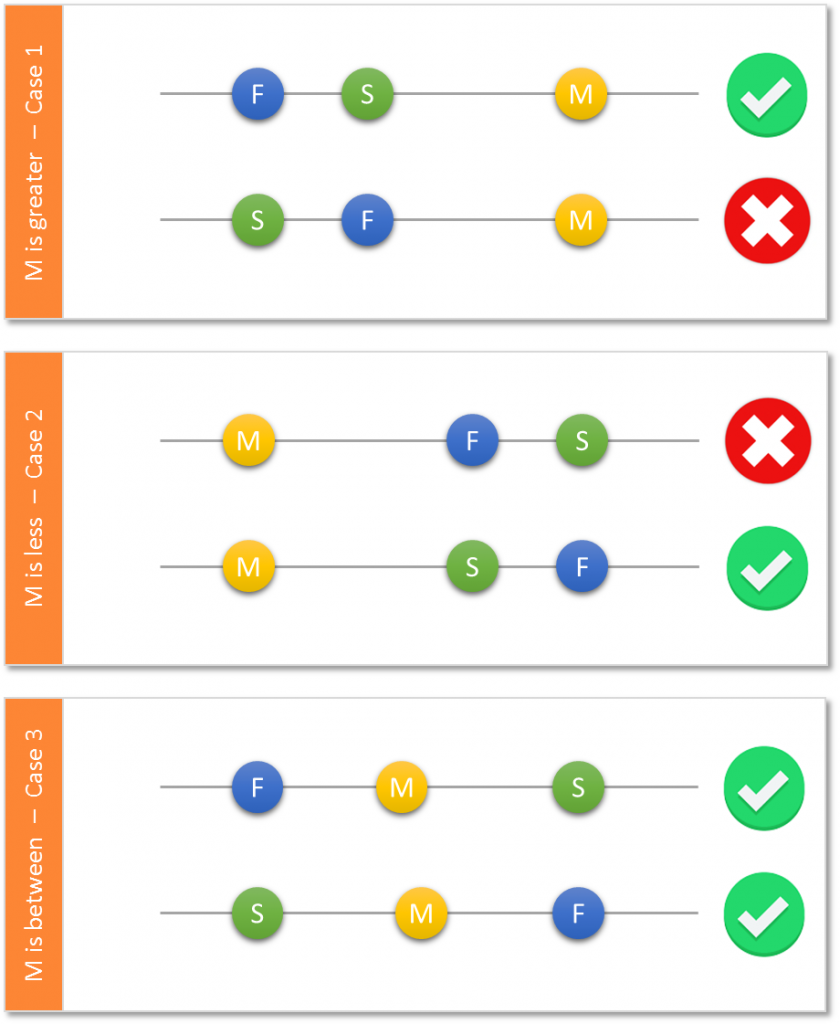
There are 6 constellations with 3 positions which can be taken by M. Only in two out of six you lose!
As you can see, we only face a 50:50 chance in case 1 and case 2. This is due to the possibility of giving a wrong guess here. However, in case 3 there is no such option. You will always win as long as your number gets between the known number F and the unknown number S. So the chance of winning has to be greater than 50% when considering all three cases!
Let P1, P2, P3 denote the probabilities that case 1, 2 and 3 occur. Since P1+P2+P3=1 we can express the probability of a successful guess PS in a mathematical manner.
Even from a mathematician’s point of view, the success probability is higher than 0.5 because P3 can only be positive 😉
Can’t believe your eyes?
But why is this outcome so counter-intuitive? People tend to think in a too abstract way. They ignore that they are given an extra piece of information, namely the first number. The above strategy makes use of the additional information while randomly guessing wastes it. Hence, you are better off when applying our guessing strategy.
I think you agree that the particular benefit of the strategy depends on M since its choice determines whether you end up in the third case. I recommend to make M equal to 10 or 20, since most people choose pairs like 2 and 87, 1 and 2834, -100 and 100… Share this fun with your friends 😀

 (7 votes, average: 4.71 out of 5)
(7 votes, average: 4.71 out of 5)





Leave a Reply