Integration by substitution (often referred to as u-substitution) is quite hard to understand. Most people just follow their proven recipe when performing this kind of integration. In contrast to that doing, I want to illustrate why the steps of u-integration are necessary. Therefore we will develop the idea slowly by giving simple examples which illustrate what works and what doesn’t.
What integration by substitution gives you
Say, you wanted to tackle an integral like the following:
You cannot integrate because the radical prevents you from doing so: Neither are you able to integrate the whole product nor does rearranging the term helps you. With however the term in the radical disappears. So substitue
. Now you have to deal with the expression
This is obviously easy to integrate. We obtain the solution
in which we can substitute back to receive the solution of the integral from the beginning of the section:
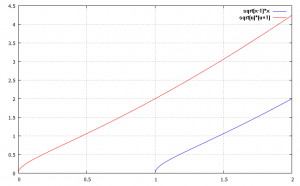
Take a look at the following picture. It clearly shows how substituting shifted the graph horizontally.
As you already have guessed, the integrals of both functions are identical. They only differ in location, but we fixed this by substituting backwars in the end. However, this procedure of simply replacing a term does not work always! (see next section)
Substituting dx – The missing factor!
Actually we omitted the substitution of up to this point. Instead we just replaced
by
which is inaccurate and works only in some special cases of integration by substitution. Let’s consider another example and try to integrate
. By the inverse chain rule, it is obvious that
But making use of the substitution and, hence,
we obtain
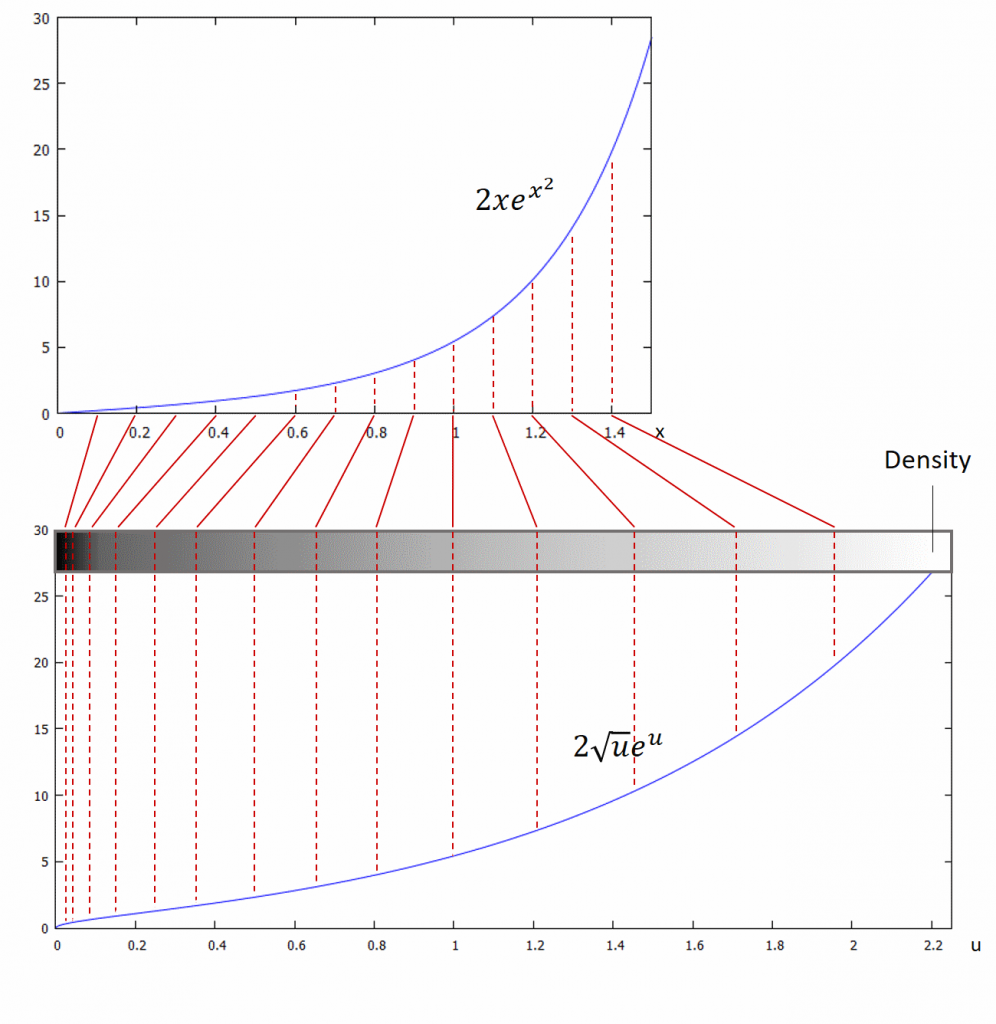
which will not lead to the desired result. So what is the probleme, here? If you have a look into the picture below then you will agree that the shape of the function is changed by substitution. The original function is much more bent upwards than the substituted version. When comparing the function values for or
respectively, you observe that the range
is compressed to a much smaller range of
while the substituted function is horizontally spread out compared to the original graph. This is also reflected in the density bar.
Of course, different shapes lead to different areas below the functions’ graphs. To overcome this issue, we need to rectify the bottom graph’s integral. That is, for each slice at a low value of we need to “virtually add” some area below the graph and vice versa. The approach is to multiply by the density
which is high if
“moves faster” than
and the other way around. Hence,
and so
Note that most people would use the following inaccurate (but very handy) mnemonic to directly substitute dx:
Or if it is easier in your case, you can differentiate , reflect about
and then substitute for
:
A final example
Integration by substitution often doesn’t work solely. I will show you an example which will involve integration by parts as well. Further, the example will illustrate how to work with limits directly instead of performing backwards-substitution in the end. Here we go!
We simplify using to transform the limits and its inverse
to transform the integrand.
Simplifying and substituting gives:
Integration by parts comes in here:
You could also have substituted backwards as usual using the fact that to obtain the indefinite integral:
I hope you now agree that integration by substitution (alias u-substitution) is an easy, logical and helpful thing 🙂

 (7 votes, average: 4.43 out of 5)
(7 votes, average: 4.43 out of 5)



October 16, 2020 at 4:17 pm
I really like this explanation. Why my students ask “why does substitution work” I always show the examples of definite integrals where the dx is a constant multiple of du, and then I say “it’s a little different when the differentials are more complicated. The axes are scaled, just by variable amounts”. I’ve been looking for a visual representation for a minute, but this is the first I’ve actually found.
Hope you don’t mind me sending my students here. Thanks for the work you put into developing this!
October 16, 2020 at 6:26 pm
It’s great that it helps your students!
March 8, 2021 at 1:13 pm
Awesome explanation I had asked this to my teachers for which i was given the answer it comes back to the original form at last. Math stack exchange is awesome which brought me here
March 10, 2021 at 7:49 am
Thanks, I am glad to hear this 🙂