Arc length of a function

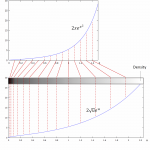
There are many applications for the arc length of functions. I came across it when I needed to calculate the length of a density function in an interval $[a,b]$ . The formula reads

$\displaystyle s=\int\limits_{a}^{b}\sqrt{1+\big[f'(x)\big]^{2}}\,dx$

Do you grasp how this formula arises? No? Let me show you!

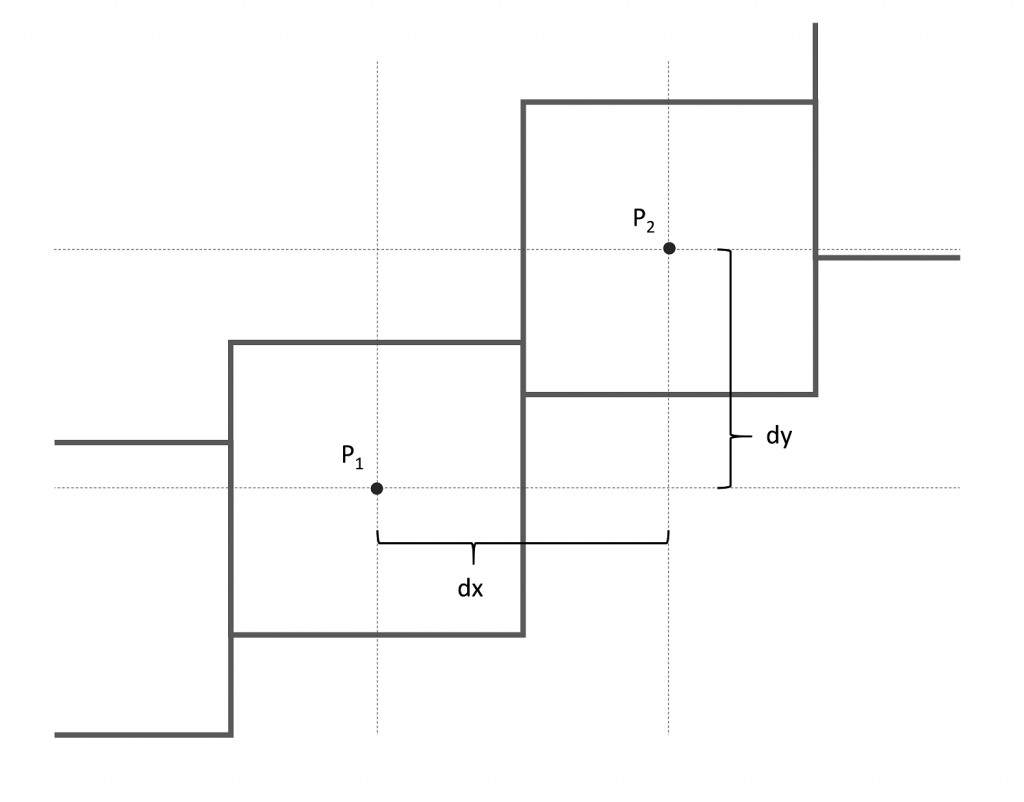
I imagined how I zoom into a function $f(x)$ until single points become visisble. Actually, this is not possible from a mathematical point of view – but let’s try for simplicity’s sake 🙂 The following sketch shows what I mean:

Grid of infinitesimal points

As you see, the horizontal distance is denoted by $dx$ while the vertical distance is denoted by $dy$ . $dy$ can be expressed in terms of $dx$ and the derivative $f'(x)$ :

$\displaystyle dy=f'(x)\cdot dx$

At the same time, Pythagoras’ theorem holds and allows us to calculate the infinitesimal distance $ds$ . I also applied some manipulations to the expression.

$\displaystyle ds=\sqrt{\big(dx\big)^{2}+\big(dy\big)^{2}}=\sqrt{\big(dx\big)^{2}+\big(f'(x)\big)^{2}\cdot \big(dx\big)^{2}}=\sqrt{1+\big(f'(x)\big)^{2}} \, dx$