It was really surprising for me when I thought about this kind of operation, namely division by arithmetic means and expected values. People tend to work with means and expected values very intuitively. You can add and multiply them without any issues. Dividing on the other hand can be misleading and I am going to illustrate this with some neat examples.
Car Acqusition
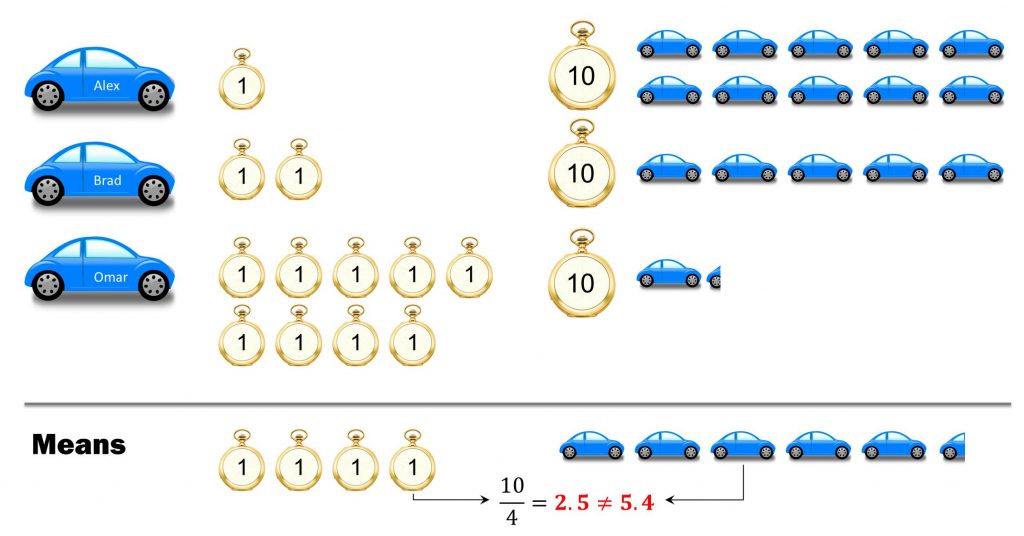
Say, in your local newspaper you read an article on the rate of car acqusition in your country. A study shows that car owners hold their car for four years on average. The title of the article reads “Car Acquisition: 2.5 cars in 10 years”. Is this deduction valid?
Take a look at the graphic below. It shows a simplified version of such a study invloving a population/sample of three people. You may recognize that the average time between two buys amounts to 4 years. However, the count over a ten years period is not the presumed 10/4=2.5 but 5.4!
It becomes obvious that the reciprocal of a mean is very different from the mean of the reciprocal values when analyzing the formulas of both:
So take care when performing such calculations!
Capacity of Muffin Production
You have not heard of Andrews Muffins yet? Andrew is a baker and you find his most popular products in the graphic below. Since he visited some statistics courses in college, he keeps the accounts to deduce useful information. He knows that he can expect a muffin to take 2.5 minutes in production (including portions of time for pastry, baking, packaging, …) under the assumption that his product mix of “Simple Muffin”, “SmartiesⓇ Muffin” and “Cherry Muffin” lasts.
Now, to optimize his pricing model, Andrew needs to know how many Muffins he can expect to produce each hour. The equation
should lead him to the expected throughput on an hourly basis, he guesses. Are you suspicious of the solution n=24? Don’t be.
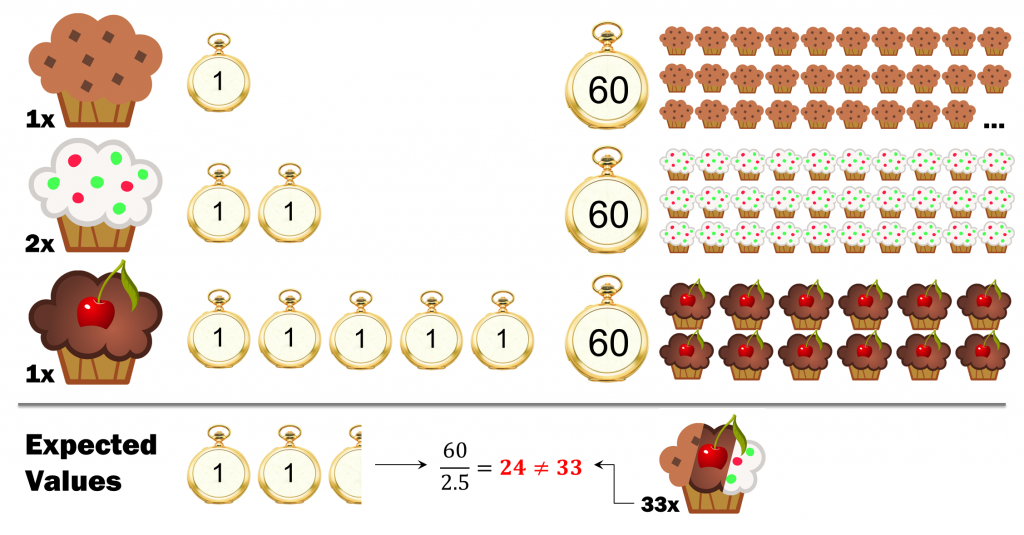
The product mix for which the expected production capacity is different from the reciprocal of the expected production time
In this particular case we should indeed agree to the left-hand solution. Wonder why? Other than in the previous example (concerning car acquisition) we deal with categories of fixed proportion here. Since 30 of 60 minutes are needed for 6 “Cherry Muffins”, Andrew is only able to produce 24 muffins per hour. You recognize that it is not possible to forbid division by means and expected values in general.
However, we usually speak about uncategorized counts. Here we can state (similar to the car acquisition example) that:
Further implications
Although distinguishing between being allowed to divide and being not allowed is hard enough, we didn’t take a look at combinations multiple random variables yet. The reciprocal is always involved when dividing by means or expected values since
As a consequence, you need to see that often
You may meet such problems in a variety of situations. Here are some examples.
- Let X denote weekly income and let Y denote weekly working hours. Then Z is not in general a valid estimate of income per hour.
- Let X denote the water consumption generated by residents of a hotel room and let Y denote the number of days for which the hotel room is booked. Then Z is not a valid estimate of water consumption per time in which the hotel room is booked.
- Let X denote the mass of a bag of cookies and let Y denote the mass of a single cookie. Then Z may not be a valid estimate for the number of cookies in the bag.
You are going to meet more examples in your everyday lifes. Often it needs a lot of caution to spot these little but highly influential mistakes. I would enjoy reading your experiences in the comment section below!





May 26, 2016 at 4:40 am
It’s like with people guessing that being 10% faster equals taking 10% time less. Try to explain that to someone in a meeting 🙂