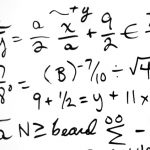Integration by substitution (often referred to as u-substitution) is quite hard to understand. Most people just follow their proven recipe when performing this kind of integration. In contrast to that doing, I want to illustrate why the steps of u-integration are necessary. Therefore we will develop the idea slowly by giving simple examples which illustrate what works and what doesn’t. more →
Insight Things
A scientific blog revealing the hidden links which shape our world
Category: Mathematics
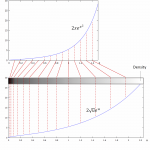
There are many applications for the arc length of functions. I came across it when I needed to calculate the length of a density function in an interval . The formula reads
Do you grasp how this formula arises? No? Let me show you! more →
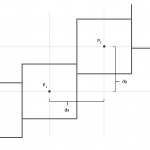
I’ve already explained in a demonstrative way how the formula for sum squared numbers arises. Not only will I only show in this article how to calculate simple series like 1+2+3+4+…., but you will also see how we enhance our findings to tackle more complicated series like 1³+2³+3³+…. These formulas are applied in many different contexts. more →
Have you ever wondered how the formula for the sum of squares (1+4+9+16+25+…) arises? Then this article is for you! We will see that there is a geometric interpretation for the problem of adding squared numbers. This interpretation will lead to the well-known formula (see “Sum of Squares, Cubes and Higher Powers” for higher powers). Curious? Then don’t let us waste time but start! more →
© 2026 Insight Things
Theme by Anders Noren — Up ↑