Paradox when rolloing a coin - Lincoln upside down

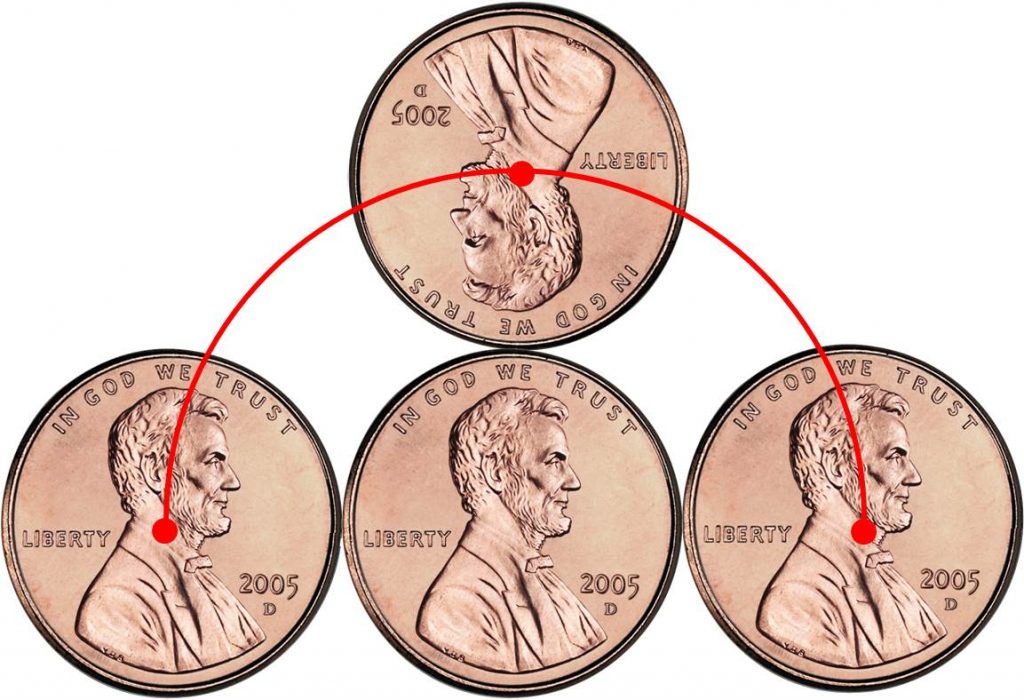
Those of you who have read previous articles of mine already know that I like tricky questions – especially if they don’t look too complicated in the first place. Here’s one for you to try: Does the penny make a half or a full rotation when rolling it around another penny?

Would you expect Mr Lincoln to show his head upside down?

Solution by demonstration

If you ask 100 people, then you can expect about 50 people emotionally arguing for the one option and 50 for the other. A reason might be that only half of the outer coin has contact to the inner coin. So, a lot of people tend to say that the coin performs only half of a rotation. The easiest way to obtain the correct solution is by trying it yourself!

The red marked coin edge illustrates the motion of the outer coin.

Obviously, the full rotation (which is the correct solution!) doesn’t require Lincoln’s breast to hit the other coin. This is due to the fact that what looks like a rotation to us consists of two parts: Revolution (rotation about the inner circle’s center) and a real rotation about its own center.

An advanced solution

This solution interesting, because it makes use of the idea that a round object’s rotation about its own center only depends on the way travelled by its center (assuming that it doesn’t slip at some point).

The red semi-circle shows the way which the center of the coin travels

Denoting the radius of the coin by $r$ , the circumference of the red semi-circle in the above figure simplifies to

$\frac{1}{2}\times 2\pi \times 2r=2\pi r$

The result of the calculation gives the distance which a single coin needs to be rolled on a straight line in order to perform the same rotation. And surprise: It implies that the coin rotates once about its center.

Straighten the semi-circle gives the equivalent distance travelled

Yet, it’s an assumption that both ways are always equal (although it appears to be perfectly logical if you think about it for some time). I hope that I will be able to provide some formal proof on this transformation in a future article. This might be interesting for solving similar problems. So, keep reading 😉