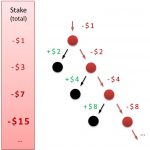
It was really surprising for me when I thought about this kind of operation, namely division by arithmetic means and expected values. People tend to work with means and expected values very intuitively. You can add and multiply them without any issues. Dividing on the other hand can be misleading and I am going to illustrate this with some neat examples.
Insight Things
A scientific blog revealing the hidden links which shape our world
Page 2 of 4
Imagine that a friend of yours would like to play a game. Your friend writes down two different numbers on two separate slips which you cannot spot. Afterwards you are allowed to choose one of the slips and read the number written on it. The game’s goal is to make a rough guess on the value of the second number.
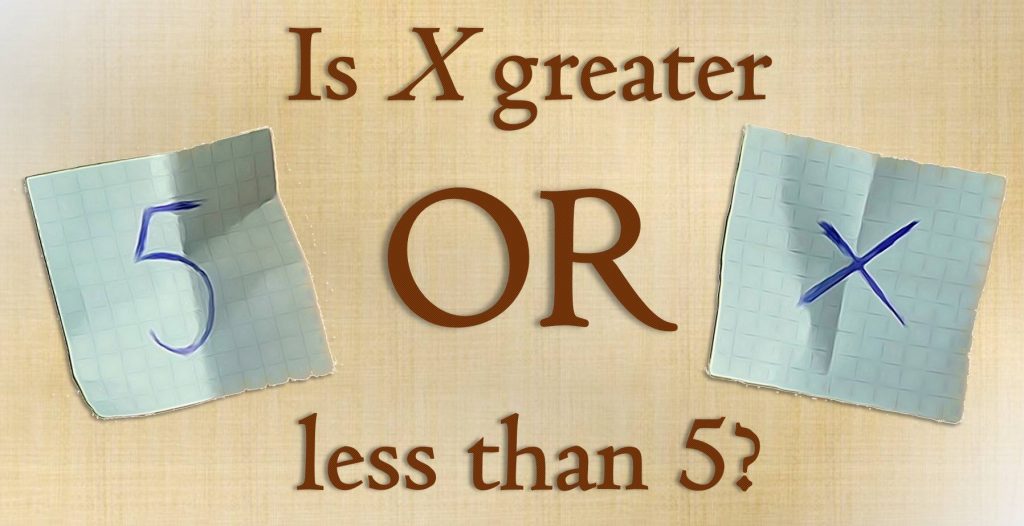
You think there is a 50:50 chance for guessing correctly? Although you may not believe it: The probability for a success is definitely higher when you apply the following strategy! more →
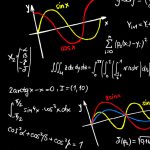
I guess that you already know a little bit about hypothesis testing. For instance, you might have carried out tests in which you tried to reject the hypothesis that your sample comes from a population with a hypthesized mean µ. As you know that the sample mean follows a t-distribution (or the normal distribution in case of huge samples), you can define a rejection region based on a specific significance level α. In a one-sided test, sample means which are less than a critical value CV might be considered to be rather unlikely. If the obtained sample’s mean falls into this region, the hypothesis gets rejected at this particular signficance level α.
Distribution of sample mean and rejection region for one-sided test
We know the chance of rejecting the hypothesis although it’s true (Type I error), because it is the chance of obtaining just one of those values from the rejection region (plotted red). But how likely are we to reject a hypothesis if it’s indeed false? In other words: How small is the type II error? more →
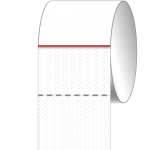
One day when I spent some day in the smallest room of my company, I really got annoyed by the toilet paper getting ripped off after the first piece of paper. Maybe you have also experienced this, especially when a toilet paper dispenser like the one shown below is involved.
Toilet paper dispenser showing unpleasant behaviour
There is kind of an unwind impediment integrated in these dispensers which makes you pull hard on the loo paper. That’s why it becomes so evident that the position where the toilet paper breaks is influenced by how you pull it. Anyway, the following explanations account for usual toilet paper consumption as well 😉 more →
Integration by substitution (often referred to as u-substitution) is quite hard to understand. Most people just follow their proven recipe when performing this kind of integration. In contrast to that doing, I want to illustrate why the steps of u-integration are necessary. Therefore we will develop the idea slowly by giving simple examples which illustrate what works and what doesn’t. more →
My dad told me that a car’s fuel economy is bad in winter, because the engine has to heat a lot more. Well, I read about cold engines, low tire pressure, higher rolling resistance and so on. They didn’t convince me. All together have a substantial impact, I admit, but the most important factor of fuel consumption is not discussed sufficiently! more →
Imagine you drive in your car against head wind and later you return with tail wind. When asked, most people tend to say that the force of the wind on average equals the situation when there is no wind at all. This is surprising since the same people will tell you that the air resistance (the aerodynamic drag) increases as the squared velocity increases. I will show you why wind is substantial when discussing causes of high fuel consumption! more →
© 2024 Insight Things
Theme by Anders Noren — Up ↑