Back in 2010, I visited a casino for the first time with some of my friends. I suggested to try a roulette strategy which I heard about earlier. It advices to “double stakes”. We earned almost 30 bucks within an hour. Let me explain what we did!

Double Stakes

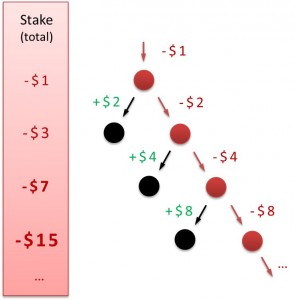
At the roulette table, we bet on black or red and doubled stakes each time we lost. For instance, we bet $1 on black and lost. Then we started another attempt, bet $2 and lost again. With the next attempt our stake grew to $4. Consider that black appeared and we won $8. Our total stake amounted to $7 and subsequently our profit totaled $1. This kind of betting system is called a Martingale. And trust me: You will always win your initial bet back when gambling until your color wins. However, there are constraints which might prevent you from coming to that crucial point!

Risks

You may guess that your stakes are going to explode, don’t you? Take a look at the graphic below. Your stakes grow exponentially and – even worse – they sum up in the total stakes. So you run the risk of either losing all your money or reaching the table limit before your color appears!

How your total stake rises when you double stakes each time you lose

How your total stake rises when you double stakes each time you lose

As we have seen so far, you can earn a low amount of money with high probability. Unfortunately, you could also lose a very large amount with low probability. But what will you earn on average?

Expected Profit

The amount you will gain in the long run can be calculated using a geometric series. It takes some mathematics, but it’s woth the pain 😀

Let n>1 be the number of rounds you play roulette and let T_{1} denote your inital bet ($1 for example). The total stake T_{n} is the partial sum of a geometric series.

\displaystyle T_{n}=\frac{1-2^{n}}{1-2} \times T_{1}=(2^{n}-1) \times T_{1}

As you double your stakes n times, you will also earn the 2^{n} fold of your inital stake T_{1} in total. These earnings are drastically reduced by the total stakes which you already invested. Your profit P remains stable whatever number of rounds you play:

\displaystyle P=2^{n} \times T_{1}-(2^{n}-1) \times T_{1}=T_{1}

In the first section I already pointed out that you will soon be bankrupt or face the table limit when playing this Martingale. The mentioned situation may occur in any round n. Weighing the chances of winning T_{1} before against the risk of losing T_{n} in the n-th round is reflected by the expected value.

\displaystyle \mathrm{E}(X)=T_{1} \times P\big(X<n\big) + T_{n} \times P\big(X=n\big)

\displaystyle \mathrm{E}(X)=T_{1}\Big(1-\left(\frac{1}{2}\right)^{n}\Big)-(2^{n}-1) \times T_{1} \times \left(\frac{1}{2}\right)^{n} = 0

Conclusion: No matter what round n it hits you, on average you will make no profit!

You cannot beat the house!

Depending on which kind of roulette game you take part in, you could even lose money. While european roulette handles the zero neutral (from a statisticians point of views), American roulette will let you lose – and therefore reduce the average profit to some value below zero 🙁

Keep in mind that roulette has not been designed to make you rich… unless you are the casino’s owner 😀