Imagine you drive in your car against head wind and later you return with tail wind. When asked, most people tend to say that the force of the wind on average equals the situation when there is no wind at all. This is surprising since the same people will tell you that the air resistance (the aerodynamic drag) increases as the squared velocity increases. I will show you why wind is substantial when discussing causes of high fuel consumption!
Illustrating the problem
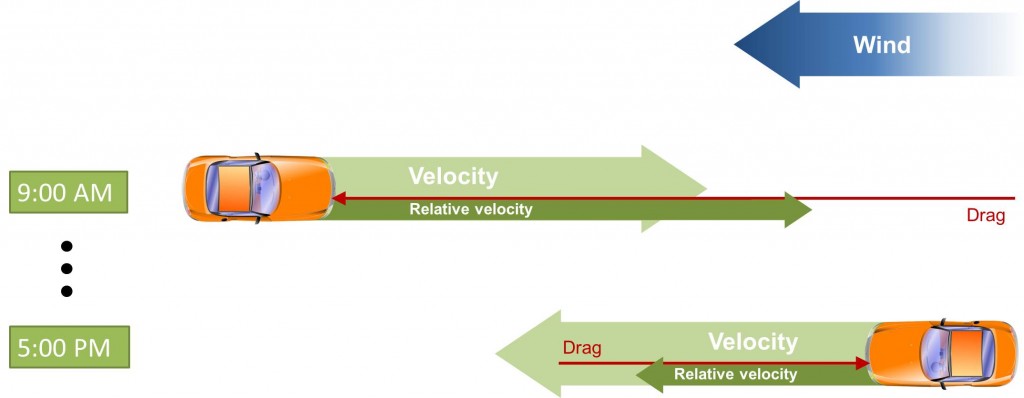
The following graphic shows the process which I described above. In the morning the car moves at the same velocity as in the evening. We assume that wind direction and intensity don’t change. Relative to the wind’s velocity, the car drives at higher speed in the morning. Due to the non-linear relationship between velocity and drag, the additional fuel consumption in the morning is much higher than the saved fuel in the evening. Hence, the average fuel consumption increases!
It is also possible to analyze the problem from a scientific point of view. Let’s investigate the issue in more detail 😉
Air resistance explained
You can calculate the aerodynamic drag force of a car when knowing its frontal area
, its velocity
, the air density
and the drag coefficient
.
Or as a function of wind velocity:
Now, we need to modify the formula to suit our situation involving wind velocity . We can give the additionally needed drag force when travelling both ways
by subtracting the forces of both directions from each other and divide by two (to calculate the mean).
There is an obviously linear relationship between the extra drag force and both types of velocity. So, wind does increase you fuel consumption – but to what extent?
Effects on fuel consumption
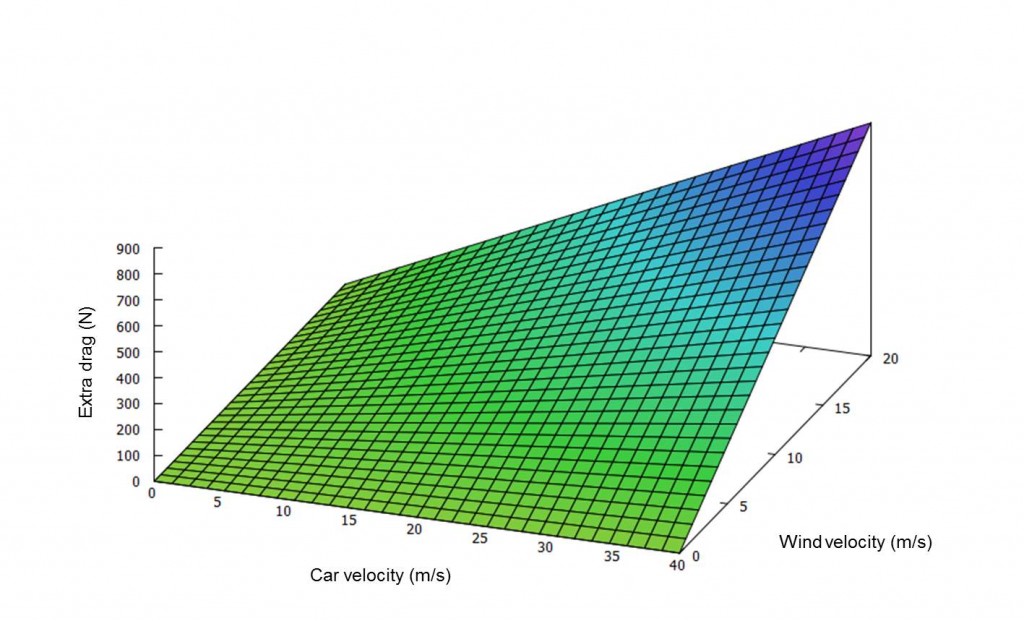
At a frontal area of 1.88m², air density of 1.22 kg/m³ and a drag coefficient of 0.32 (which are quiet good values!), we can show the extra force, that your engine has to provide, in the following graph.
Bear in mind, that due to the energy density of petrol and motor efficiency 100N result in up to 0.8 liters per 100km of additional fuel (depending on the exact wind direction). For instance, going at 120km/h (75mph) with wind blowing at an average of 20km/h (12.5mph) means an extra consumption of about 1.6 liters! And it gets even worse in winter, when air is denser…







Leave a Reply