One day when I spent some day in the smallest room of my company, I really got annoyed by the toilet paper getting ripped off after the first piece of paper. Maybe you have also experienced this, especially when a toilet paper dispenser like the one shown below is involved.
There is kind of an unwind impediment integrated in these dispensers which makes you pull hard on the loo paper. That’s why it becomes so evident that the position where the toilet paper breaks is influenced by how you pull it. Anyway, the following explanations account for usual toilet paper consumption as well 😉
Modelling the toilet paper
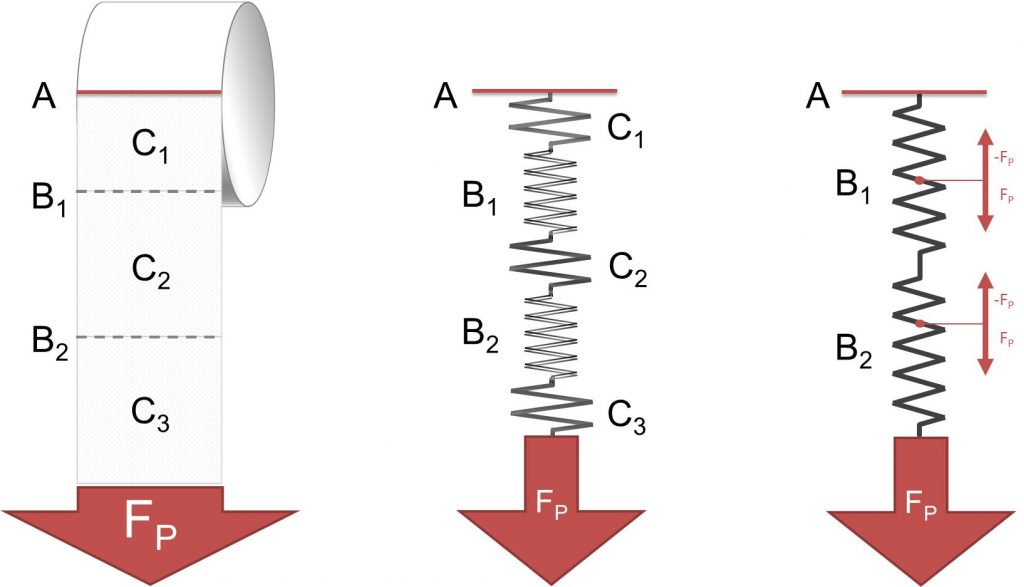
The first challenge that I faced was the modelling process. From my point of view, comparing the components of the toilet paper with mechanical springs makes pretty much sense. See the picture below. There is a line at which the paper leaves the roll (A). In terms of mechanics, the upper spring is fixed at A. Individual perforations (B1, B2, …) and pieces of toilet paper (C1, C2, …) are represented by springs. You’ll agree that a perforation is much more elastic than the paper. Therefore I abolished the representation of the paper in the final step of the modelling process.
The analogy regarding mechanics obviously shows that the pulling force FP at each position between your hand and the roll in case you pull uniformly. Each perforation’s tension can in turn be modelled: The pulling force is distributed uniformly along the perforation.
A conclusion? Right: As the tension in the perforation is equal at every position of the profile, there is no minimum and no maximum. Hence, the perforation’s maximal tolerated tension doesn’t get exceeded and therefore the toilet paper is most unlikely to get ripped off at all in this case.
Where toilet paper gets ripped off
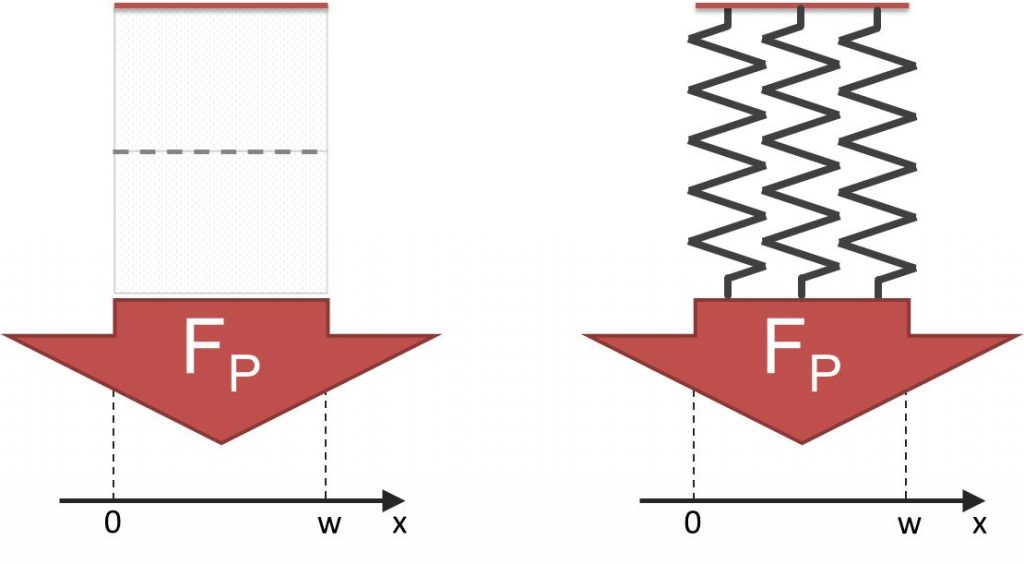
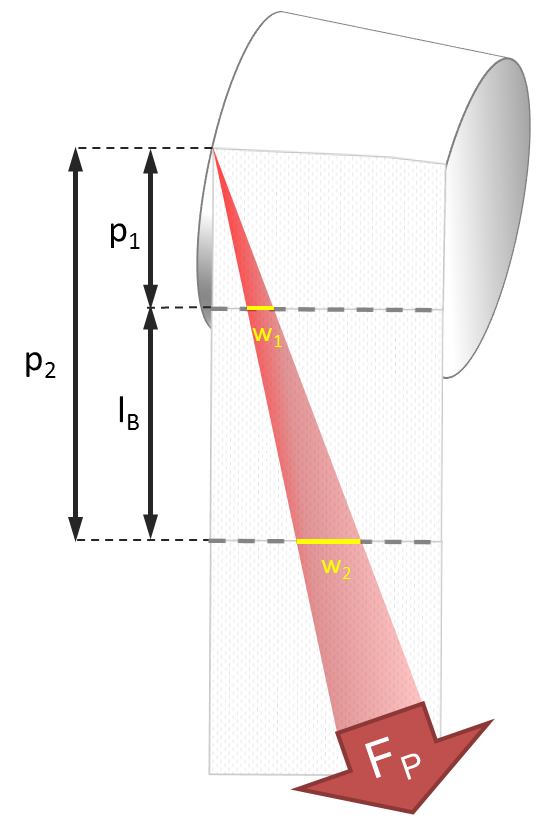
From a practitioner’s point of view, there are two more interesting cases: Pulling straightly and pulling skew. ‘Pulling straightly’ means that you pull in one point. The pulling force FP gets distributed (and therefore the tension decreases) as you go along the chain of papers towards the roll. Indeed the tension follows a cosine function, but you can approximate it by applying the intercept theorem (ask for further details if you are interested 😉 ). Hence the toilet paper will probably get detached after the first piece of paper, since tension is the highest here.
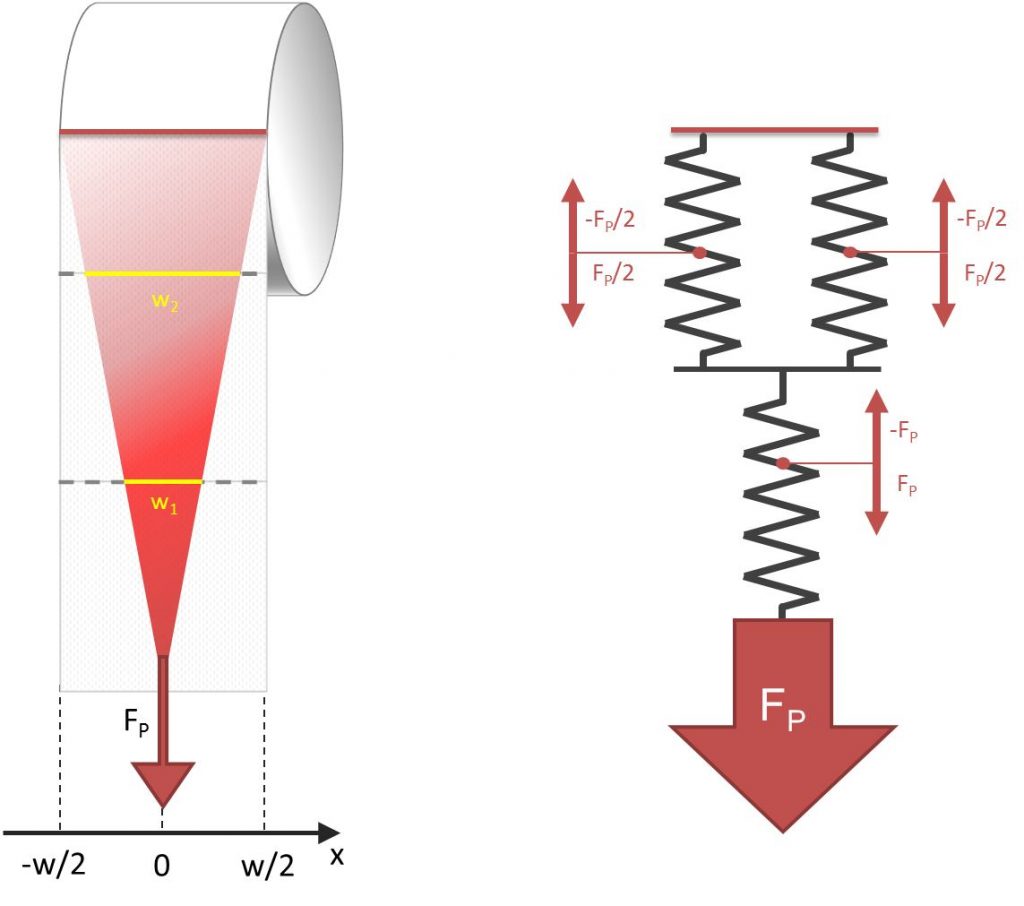
The second case is also interesting. Consider you pull to the right. Then a point at the left-hand side, where the last piece of tissue leaves the role, arises. Since your finger has some width but the point doesn’t, the force gets concentrated more and more in direction to the roll. You can (approximately) calculate the tension in the perforation by applying the intercept theorem again. Apparently, the toilet paper will be divided at the roll with high probability. And be careful: The tension is the highest of all cases which might cause unexpected breaks!
Conclusion
If you don’t want your toilet paper to break after the first piece of paper, you should try to pull in many points similar to the case of the modelling section. First pull skew when you have yielded enough pieces of paper, because the toilet paper will probably break when doing so. Make the most of it 😀








Leave a Reply