Have you ever wondered how the formula for the sum of squares (1+4+9+16+25+…) arises? Then this article is for you! We will see that there is a geometric interpretation for the problem of adding squared numbers. This interpretation will lead to the well-known formula (see “Sum of Squares, Cubes and Higher Powers” for higher powers). Curious? Then don’t let us waste time but start!
An analogy for the sum of squares
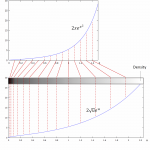
The sum of squared numbers can be thought of as the volume of a pyramid built from square panels of height 1. I will refer to them as ‘bricks’. The picture below illustrates this idea.
Calculating the volume of this 'brick pyramid' is actually not easy, because there is no formula right away. However, as shown in the above picture, you can design a normal pyramid around the brick pyramid. This outer pyramid will intersect only with the upper corners and edges of the brick pyramid. Fortunately, there is a formula to calculate the volume of the outer pyramide. The only thing left to do, is calculating the difference between the outer and inner pyramid.
Filling the corners
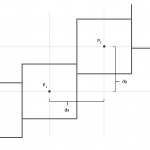
The gap between both pyramids consists of several edges and corners. An example for each can you see in the picture below.
Let’s begin with the corners. Each corner is a (skew) pyramid itself with square base of size and height
. Therefore, the volume of each corner is given by
There are layers and we need to place 4 corners at each of them. Plus a spire of course. 😉
Filling the edges
Let’s put focus on thedges now. They need some more maths than the corners. Maybe you have noticed that each edge looks like a prism with triangled base. When you break each edge into units of width 1 then their volums will equal
When moving from the top of the brick pyramid downwards, the edges’ widtsh are going to increase. The number of units needed on each side of the pyramid can be calculated using the arithmetic series 1+2+3+4+…+n. Just use the following formula (or see here how it arises).
As the pyramid consists of 4 sides, we multiply by four.
Result
Now, we are going to bring it all together.
.
Just have a second look at the first picture presented in this article. The volume of the outer pyramid has not been given yet, but the calculation can be accomplished using the general volume formula for pyramids where is the base area and
is the height of the pyramid.
Substituting this result into the formula for the volume of the block pyramid gives
To save some time, I let Maxima – the CAS which I trust – simplify this expression.
This is the formula which you will also find when looking up the sum of the first squared numbers at Google. But now you also have a clue how to explain it 🙂







October 24, 2016 at 3:02 pm
Wouldn’t it be easier to align the pyramid along an imaginary cube sort of like this: http://www.jacobtyler.com/app/uploads/2015/05/aops-logo.jpg
October 29, 2016 at 6:09 pm
I am very interested in your idea. Could give some details on how you would align the pyramid along this cube?