Are you also annoyed when it comes to parking your car? I asked myself, whether marked parking spots are rather hurdles than helpers, and wrote this article 🙂 The goal is to investigate what’s better: Marked or unmarked parking space?
Features of (un)marked parking spots
It is not a secret that the maximum number of parking cars is fixed on a parking lot with marked parking spaces. The distance between the cars, on the other hand, is flexible. In this way, marked parking spaces penalize owners of fat cars 😉
The opposite applies to unmarked parking spaces. Your car might be broad as hell and you will still have an appropriate distance to the cars around you. Friends of unmarked parking spaces argue that the available space on the parking lot will be the same as with marked parking spaces on average, but in case there are many small cars then the additional space can be used by others. Is this true? We will find out!
A serious investigation on parking space
Imagine a row in a parking lot with 50 marked parking spaces. Each parking space is of width 2.50 meters. Assuming that the average car takes 1.80 meters, the distance between two cars will be 0.70 meters (on average). The width of the parking row adds up to 125 meters. It will serve as benchmark.
Now imagine a row, 125 meters in width, in a parking lot without markings. On average there is space for 50 cars as well. However, we want to investigate the probability that one or more additional cars find a parking space. For this purpose let’s take a look at the distribution of total width for 51 cars. The expected width equals . I performed some investigation and found that the variance in car width equals approximately
. The variances for the 51 cars sum up to
, which represents total width’s variance for 51 cars. By the central limit theorem, we can assume a normal distribution when adding the random widths.
Below you find a diagram showing the corresponding probability density function. If you want all 51 cars to find a place, then the total width must lie somewhere in the red area. I could have drawn the red area proportionally, but you wouldn’t see it. The exact value can be computed using R and is actually almost zero!
pnorm(50*2.5,mean=51*2.5,sd=sqrt(51*0.1^2),lower.tail=TRUE)
[1] 0.0002320188
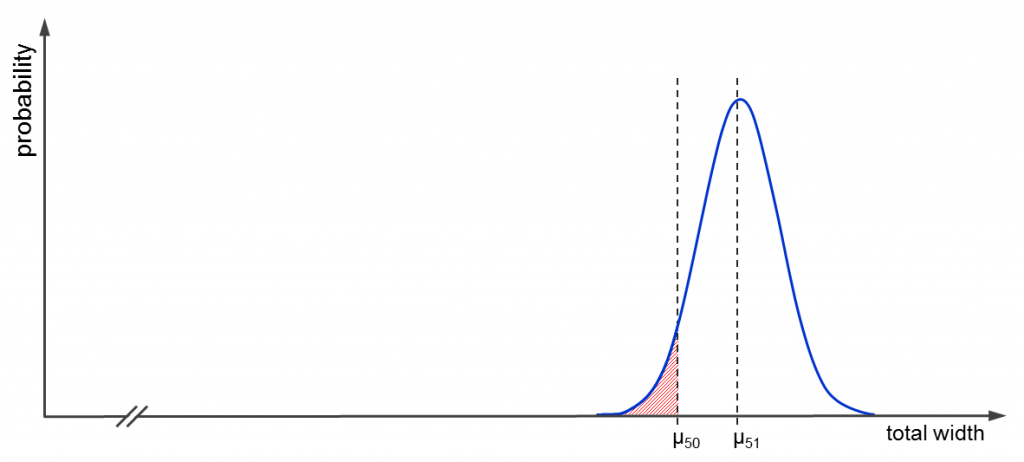
Probability density for 51 cars with the probability marked that they find their place in less than 125m
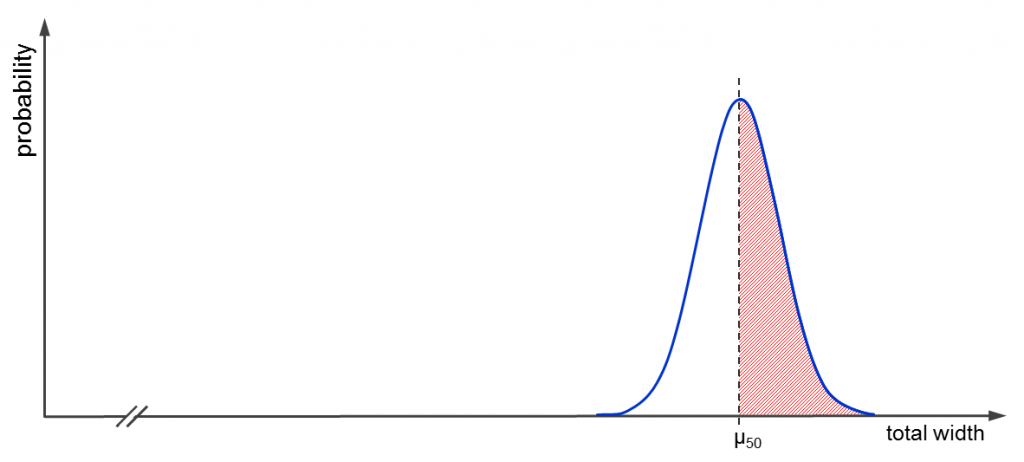
And what about the downsides of unmarked parking? Consider the distribution for 50 cars with expected total width and variance
. As soon as more than 125 meters are required, at least one car less can park. Unfortunately, this is the case 50% of the time. 😀
We conclude: The disadvantages of unmarked parking spaces outweigh the benefits!
A word on parking practice
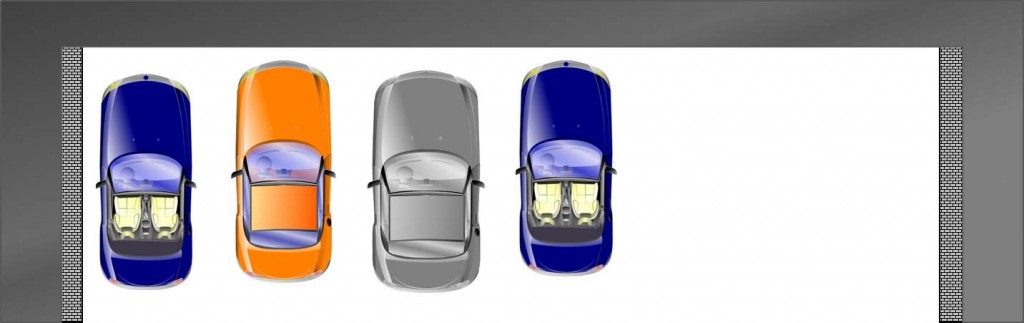
We have seen that unmarked parking spaces are not advantageous so far. Things look even worse when you visit some parking lot without markings. You will observe a situation like illustrated in the following picture.
Have you noticed the giant spaces between the cars? Such a fragmentation arises from the difference in car sizes. A broad car might not fit in the space a small car left, for instance. Moreover, people will claim more space than actually required, if you let them. Last but not least, cars on unmarked parking lots waste space in that they stand crooked.
All in all, we should be grateful that there are markings on many parking lots 😀











Leave a Reply